浅析排序算法

浅析排序算法

运行环境

​ 本文所有程序都使用Java语言编写，JDK版本为15，程序运行环境为Windows 10 + IntelliJ IDEA 2020.2.2 (Ultimate Edition)。数据的类型为int，统一使用数组存放。

排序算法的简介和实现

直接插入排序

​ 插入排序是一种简单直观的排序算法。其实现步骤是：

  • 从头到尾遍历数组来构造有序数组，对于未有序数据，从尾到头对有序数据进行遍历，然后插入相应的位置。

​ 直接插入排序方法中，使用len变量存放数据的长度，index记录被操作数据的当前位置。不断交换前后两数在保证有序数组不被打乱的情况下，将待排序数据插入对应位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 插入排序
public void insertSort(int[] data){
    int len = data.length;

    for(int i = 1; i < len; i++){
        // 使用交换法插入到对应的位置
        int index = i;
        while(index > 0 && data[index] < data[index-1]){
            // 异或交换两数
            data[index] = data[index] ^ data[index-1];
            data[index-1] = data[index] ^ data[index-1];
            data[index] = data[index] ^ data[index-1];
            index--;
        }
    }
}

希尔排序

​ 希尔排序也是一种插入排序，是在直接插入排序的基础上进行改进后得到的更高效的版本，也称为缩小增量排序。希尔排序的实现步骤为：

  • 把数据按一定的增量分组，对每一个组别进行直接插入排序

  • 然后缩小增量，再重复上面步骤，直到增量为1时，所有数据被分为一组，再进行最后一次排序，即完成排序。

​ 其中增量的取值和增长速度直接影响希尔排序的效率。

​ 希尔排序方法中，group为增量。组内排序使用直接插入排序。由于一个数据总是有序的，所以每一次大循环从第group+1个数据，也就是下标为group的那个数据开始。间隔为group的数据都属于同一个组，所以组内的上一个数据为temp – i，这里的temp用来临时存放被操作数据的下标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 希尔排序
public void shellSort(int[] data){
    int len = data.length;
    int group = len / 2;

    while(group > 0){
        // 对每一个组别进行一次插入排序
        for(int i = group; i < len; i++){
            int temp = i;
            while(temp-group >= 0 && data[temp] < data[temp-group]){
                // 异或交换两数
                data[temp] = data[temp] ^ data[temp-group];
                data[temp-group] = data[temp] ^ data[temp-group];
                data[temp] = data[temp] ^ data[temp-group];
                temp -= group;
            }
        }
        group /= 2;
    }
}

简单选择排序

​ 选择排序是表现最稳定的排序算法之一，无论是什么样的数据都是O(n2)的时间复杂度。虽然稳定但是花费时间长，不适合规模大的数据。其实现步骤是：

  • 遍历未有序数据，从中找出最小或最大的值，把它放在有序数据的尾部。

  • 重复上面步骤，知道所有数据都有序，排序完成。

​ 简单选择排序算法中，maxIndex存放最大数的下标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 选择排序
public void selectSort(int[] data){
    int maxIndex;                 // 存放最大数的下标
    int len = data.length;
    for(int i = 0; i < len; i++){
        maxIndex = 0;
        for(int j = 1; j < len - i; j++){
            if(data[maxIndex] < data[j]){
                maxIndex = j;
            }
        }

        // 将最大的放在未排序数据的最后，如果在最后就跳过
        if(maxIndex != len - i - 1){
            data[maxIndex] = data[maxIndex] ^ data[len-i-1];
            data[len-i-1] = data[maxIndex] ^ data[len-i-1];
            data[maxIndex] = data[maxIndex] ^ data[len-i-1];
        }
    }
}

堆排序

​ 堆排序是利用堆这种数据结构设计的排序算法，堆是一个近乎完全二叉树的结构，其特点是父节点的值总是大于（或小于）子节点。其实现步骤是：

  • 将数据构建成一个堆

  • 然后将堆顶元素和堆底元素交换，并将堆底元素视为堆外。

  • 交换后的堆可能不满足堆的性质，此时需要对堆进行维护，不断交换父子节点，直到满足堆的性质。

  • 不断重复步骤2和3直到堆为空，则数据排序完毕。

​ 堆排序算法中，由于数据使用数组存储，不再采取其他数据结构来变更数据的存储，所以不用去构建堆，只需要从尾到头调整一下，跳过叶子结点。len表示堆的大小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public class HeapSort {
    static int len = 0;
    // 堆排序
    public void heapSort(int[] data){
        // 构建堆
        len = data.length;
        for(int i = len / 2 - 1; i >= 0; i--){
            adjustHeap(data,i);
        }

        // 排序
        while(len > 0){
            data[0] = data[0] ^ data[len-1];
            data[len-1] = data[0] ^ data[len-1];
            data[0] = data[0] ^ data[len-1];
            len--;
            adjustHeap(data,0);
        }
    }

    private void adjustHeap(int[] data, int node){
        int maxIndex = node;

        // 比较父节点,左右节点之间比较
        while(node*2+1 < len && data[maxIndex] < data[node*2+1]){
            maxIndex = node * 2 + 1;
        }

        while(node*2+2 < len && data[maxIndex] < data[node*2+2]){
            maxIndex = node * 2 + 2;
        }

        if(maxIndex != node){
            data[maxIndex] = data[maxIndex] ^ data[node];
            data[node] = data[maxIndex] ^ data[node];
            data[maxIndex] = data[maxIndex] ^ data[node];
            adjustHeap(data,maxIndex);
        }
    }
}

冒泡排序

冒泡排序是一种简单的排序算法。其实现步骤是：

  • 从头到尾遍历数据，如果相邻两个数据顺序不正确（根据排序规则判断），则交换这两个数据，遍历到尾部后，最后面存放的就是最小或者最大的数据，将遍历的长度减一。

  • 重复上面步骤，直到需要遍历的长度为0，排序完成。

​ 冒泡排序方法中，flag用来标记当前数据是否已经排序好，如果某一次排序，从头到尾都没有出现数据交换的情况，则数据已经排好序，可以退出方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 冒泡排序
    public void bubbleSort(int[] data){
        int len = data.length;
        boolean flag = false; // 优化，如果某一次冒泡排序没有交换，则代表已排序完

        for (int i = 0; i < len && !flag; i++) {
            flag = true;
            for(int j = 0; j < len - i - 1; j++){
                if(data[j] > data[j+1]){
                    flag = false;
                    data[j] = data[j] ^ data[j+1];
                    data[j+1] = data[j] ^ data[j+1];
                    data[j] = data[j] ^ data[j+1];
                }
            }
        }
    }

快速排序

​ 快速排序使用分治的思想来实现。其实现步骤为

  • 先选择一个基准，然后遍历数据，将所有小于基准的数据放在基准的左边，所有大于基准的数据放在基准的右边。

  • 根据基准位置，将数据分为两份子数据。

  • 子数据重复上述步骤，直到子数据的长度为1。

​ 快速排序有多种实现方法，本文采取的是双指针法，先设置头部第一个数据为基准数，尾部指针从后往前找第一个小于基准的数，找到以后，头部指针从前往后的找第一个大于基准的数，然后交换两数，直到两指针相撞，把基准数和相撞位置的数交换，这就完成一次快速排序。tempSt存放初始起点，tempEd存放初始终点，用于最后对两个子数据调用快速排序方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// 快速排序
public void quickSorted(int[] data, int st, int ed){
    // 只有一个数无须排序
    if(st >= ed){
        return;
    }

    int flag = st;
    int tempSt = st;
    int tempEd = ed;

    while(st < ed){
        // 从右到左找到第一个小于基准的数
        while(st < ed && data[ed] >= data[flag]){
            ed--;
        }

        // 从左到右找到第一个大于等于基准的数
        while(st < ed && data[st] <= data[flag]){
            st++;
        }

        // 两指针指向位置不相等则交换数字(通过两数异或实现)
        if(st != ed){
            data[st] = data[st] ^ data[ed];
            data[ed] = data[st] ^ data[ed];
            data[st] = data[st] ^ data[ed];
        }
    }

    // 异或交换不能在同一个数
    if(flag != ed){
        // 将基准插入对应位置
        data[flag] = data[flag] ^ data[ed];
        data[ed] = data[flag] ^ data[ed];
        data[flag] = data[flag] ^ data[ed];
    }

    // 对两份子数据进行快速排序
    quickSorted(data,tempSt,st-1);
    quickSorted(data,st+1,tempEd);
}

归并排序

​ 归并排序是一种采用了分治思想的稳定排序算法。其实现步骤如下：

  • 将数据对半分成两份子数据

  • 对子数据分别采用归并排序

  • 将排序好的两份子数据合并成一个完整的数据

​ 归并排序方法，由于使用数组存储，在对排好序的子数据进行整合的时候，需要多使用一个等长数组来临时存放数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// 归并排序
public void mergeSort(int[] data, int st, int ed){
    // 只剩一个数不排序
    if(st >= ed){
        return;
    }

    //将数据一分为二，分别进行归并排序
    int mid = (st + ed) / 2;
    mergeSort(data,st,mid);
    mergeSort(data,mid+1,ed);

    // 将排序好的数据进行合并
    int[] temp = new int[ed - st + 1];
    int flag1 = st;
    int flag2 = mid + 1;

    int count = 0;
    while(flag1 <= mid && flag2 <= ed){
        if(data[flag1] <= data[flag2]){
            temp[count++] = data[flag1++];
        }else{
            temp[count++] = data[flag2++];
        }
    }

    // 前半数组没遍历完
    while(flag1 <= mid){
        temp[count++] = data[flag1++];
    }

    // 后半数组没遍历完
    while(flag2 <= ed){
        temp[count++] = data[flag2++];
    }

    // 将数据赋值回去
    count = 0;
    for(int i = st; i <= ed; i++){
        data[i] = temp[i-st];
    }
}

基数排序

基数排序是非比较的排序算法，从数据的最低位到最高位进行排序的。其实现步骤如下：

  • 获得数据中最大值的位数，从最低位开始截取位值

  • 从头到尾遍历数据，利用容器来计数，计算出当前位为0-9的个数，通过这个计算出每一个数字收集后的位置，然后就数据临时存储到另一个数组，再把值赋值回去。

  • 截取的位置前进一位，然后重复步骤2，直到截取位置超过最大位数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 基数排序
public void radixSort(int[] data){
    int len = data.length;
    int maxLen = 0;
    int[] tempData = new int[len];

    // 找出最大值
    int maxNum = Arrays.stream(data).max().getAsInt();
    // 计算最大位数
    while(maxNum > 0){
        maxLen++;
        maxNum /= 10;
    }

    int rule = 1;
    for(int i = 0; i < maxLen; i++,rule *= 10){
        // 对应各位置的堆
        int[] heap = new int[10];
        // 将每个数据按位数放好
        for(int j = 0; j < len; j++){
            heap[(data[j] / rule) % 10]++;
        }
        // 累加求位置
        for(int j = 1; j < 10; j++){
            heap[j] += heap[j-1];
        }
        // 收集数据
        for(int j = len - 1; j >= 0; j--){
            tempData[--heap[(data[j] / rule) % 10]] = data[j];
        }
        // 数据回传
        for(int j = 0; j < len; j++){
            data[j] = tempData[j];
        }
    }
}

排序算法的分析比较

​ 排序算法的稳定性是指在排序过程中会不会改变相同数据彼此位置的相对次序，如果我们在使用排序算法时，不希望相同元素的次序发生改变，就得选择一些具有稳定性的排序算法，所以排序算法的分析需要从稳定性、时间复杂度和空间复杂度入手。

​ 算法在n（以下都用n来代指数据的大小规模）下的运行时间都通过程序测试方法获得：

  • 使用随机方法生成n个随机的数据，存储到数组中

  • 获取当前时间，运行方法，再次获取时间，两次时间相减获得一次程序的运行时间

  • 为了减少误差，重复获取运行时间20000次，取平均值。

直接插入排序

  1. 稳定性分析

​ 直接插入排序是稳定的，因为对数据从头到尾进行遍历，在前的数据会先被插入，由于比较的时候，只有当被操作数小于前一个数才会交换，这就保证了后面的数据不会插入被相同数据的。

  1. 时间复杂度分析

​ 直接插入排序的主要时间花费在于两个for循环。第一个for循环的次数为n-1，第二个for循环的次数是不确定的，最坏的情况每一次都需要将被操作数插到有序数据的头部，这种情况下次数是从1递增到n-1，最好的情况每一次被操作数只需要放到有序数据的尾部，这时候不需要交换，次数为0。由于插入到哪个位置的可能性是一样的，所以正常情况下，插入的次数为最坏情况的一半。则直接插入排序的时间复杂度为：

  • 最好情况:O(n)

  • 最坏情况:O(n^2^)

  • 平均情况:O(n^2^)

​ 在不同规模的情况下，使用运行程序测试方法来获取数据，将数据整合到下表

n的规模 运行时间(ms) n的规模 运行时间(ms)
1000 0.4537 5500 12.6239
1500 0.9426 6000 15.0498
2000 1.6864 6500 17.6556
2500 2.6287 7000 20.4813
3000 3.7741 7500 23.4397
3500 5.1270 8000 26.6538
4000 6.6954 8500 30.0928
4500 8.4593 9000 33.8105
5000 10.4379 9500 37.5833

根据数据绘制出对应的图像：

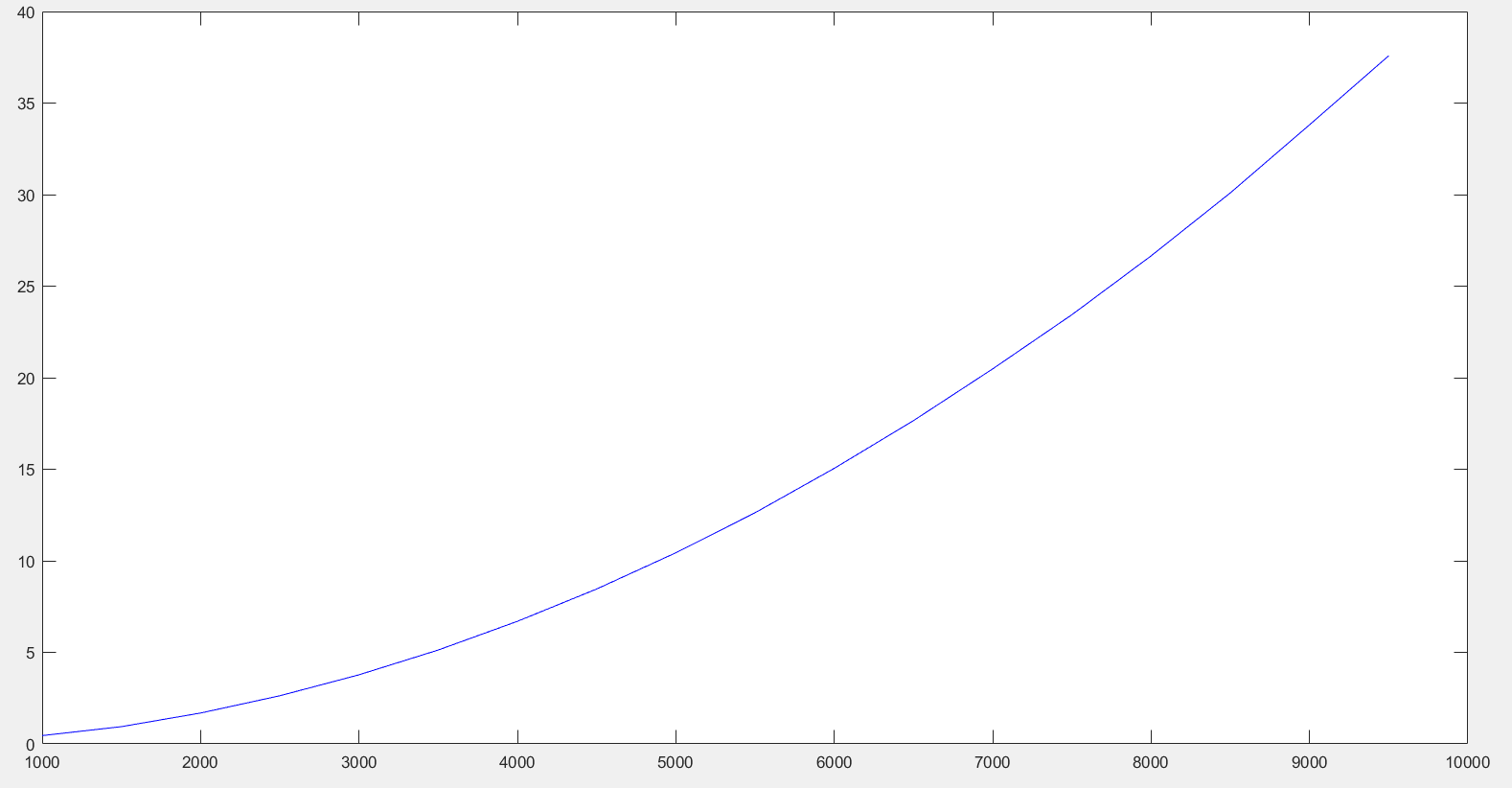
直接插入排序

  1. 时间复杂度分析

​ 直接插入排序不使用额外的空间，所以空间复杂度为O(1)。

希尔排序

  1. 稳定性分析

​ 希尔排序是不稳定的，虽然分组内部使用的是直接插入排序，但是由于希尔排序会分组，相同的数组可能会被分到不同组，这时候就无法保证原来的次序。

  1. 时间复杂度分析

​ 希尔排序时间复杂度受增量和增长速度影响，如果按照本文的实现，希尔排序的时间复杂度如下：

  • 最好情况:O(nlogn)

  • 最坏情况:O(nlog^2^n)

  • 平均情况:O(nlog^2^n)

​ 如果更换增量和增长速度来最优化希尔排序，有人通过大量的实验，当n较大时，希尔排序的比较和移动的次数约在n1.25到(1.6n)1.25之间。

​ 在不同规模的情况下，使用运行程序测试方法来获取数据，将数据整合到下表

n的规模 运行时间(ms) n的规模 运行时间(ms)
1000 0.0874 5500 0.5372
1500 0.1186 6000 0.6079
2000 0.1673 6500 0.6567
2500 0.2155 7000 0.7094
3000 0.2663 7500 0.7671
3500 0.3160 8000 0.8720
4000 0.3807 8500 0.8868
4500 0.4214 9000 0.9537
5000 0.4901 9500 1.0219

根据数据绘制出对应的图像：

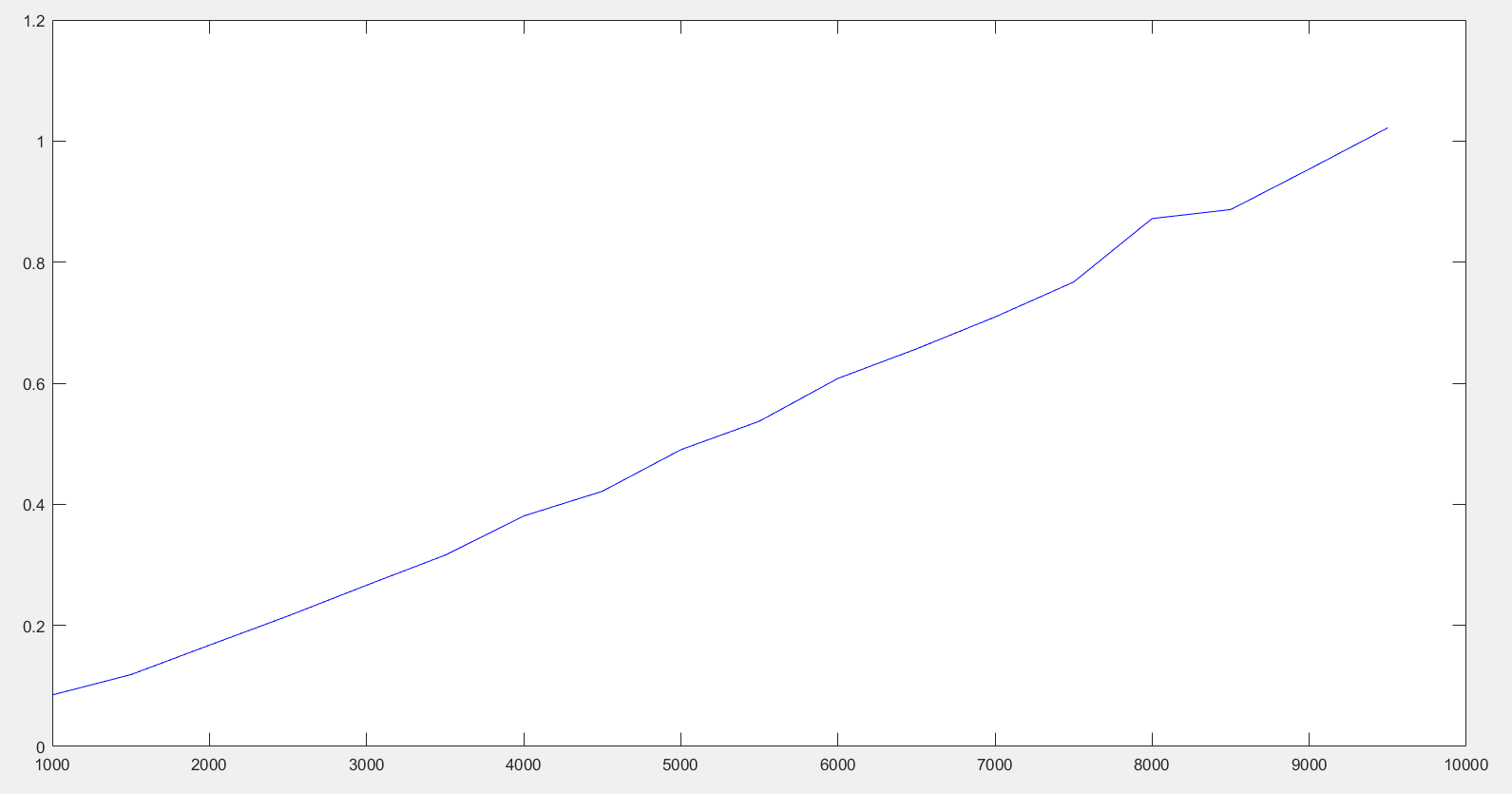
直接插入排序

  1. 时间复杂度分析

​ 希尔排序也无需使用额外内存，所以空间复杂度也为O(1)。

简单选择排序

  1. 稳定性分析

​ 简单选择排序是不稳定的，因为它会交换最小或最大数据的队首或者队尾，这样就有可能把原来在后面的数据交换到前面。例如数组[4,3,3]会将4和3进行交换，这样原来在后面的3就被排序到了前面。

  1. 时间复杂度分析

​ 简单选择排序花费的时间主要在两个for循环，第一个循环的次数为n，第二个循环的次数从n-1递减到1，所以简单选择排序的时间复杂度为O(n2)。简单选择排序很稳定，不会因为数据的不同情况而出现波动的情况。

  • 最好情况:O(n^2^)

  • 最坏情况:O(n^2^)

  • 平均情况:O(n^2^)

​ 在不同规模的情况下，使用运行程序测试方法来获取数据，将数据整合到下表

n的规模 运行时间(ms) n的规模 运行时间(ms)
1000 0.3798 5500 8.0870
1500 0.7337 6000 9.6023
2000 1.1229 6500 11.2485
2500 1.7248 7000 13.0221
3000 2.4592 7500 14.9337
3500 3.3204 8000 16.9716
4000 4.3129 8500 19.1393
4500 5.4387 9000 21.4369
5000 6.7016 9500 23.9121

根据数据绘制出对应的图像：

直接插入排序

  1. 时间复杂度分析

​ 简单选择排序也不需要额外的空间，所以时间复杂度为O(n)。

堆排序

  1. 稳定性分析

​ 堆排序不稳定的，因为堆的性质只保证堆顶元素是最大的，在维护堆的时候无法确保先把相同元素的前一个或者后一个交换上来。例如，数据[5,3,3]会交换堆顶的5和堆底的3，交换完数据变成[3,3]和[5]（5还在数组内，这里分开是表示已排序不属于堆），后面的3就被交换到了前面。

  1. 时间复杂度分析

​ 堆排序主要时间花费在于构建堆、调整堆，构建堆的时间得看采用的数据结构，本文采用数组存储，构建堆时只需要从尾到头对堆进行调整，堆一次调整最多执行logn次，最少执行0次，平均还是logn次，构建堆的时候至多需要对n个数据进行调整，所以需要nlogn次操作。需要从堆中移出n-1个数据，所以需要(n-1)logn。两者相加，堆排序的时间复杂度如下：

  • 最好情况:O(nlogn)

  • 最坏情况:O(nlogn)

  • 平均情况:O(nlogn)

​ 在不同规模的情况下，使用运行程序测试方法来获取数据，将数据整合到下表

n的规模 运行时间(ms) n的规模 运行时间(ms)
1000 0.0874 5500 0.5570
1500 0.1295 6000 0.6133
2000 0.1818 6500 0.6714
2500 0.2335 7000 0.7310
3000 0.2863 7500 0.7912
3500 0.3419 8000 0.8499
4000 0.3914 8500 0.9098
4500 0.4454 9000 0.9652
5000 0.5038 9500 1.0301

根据数据绘制出对应的图像：

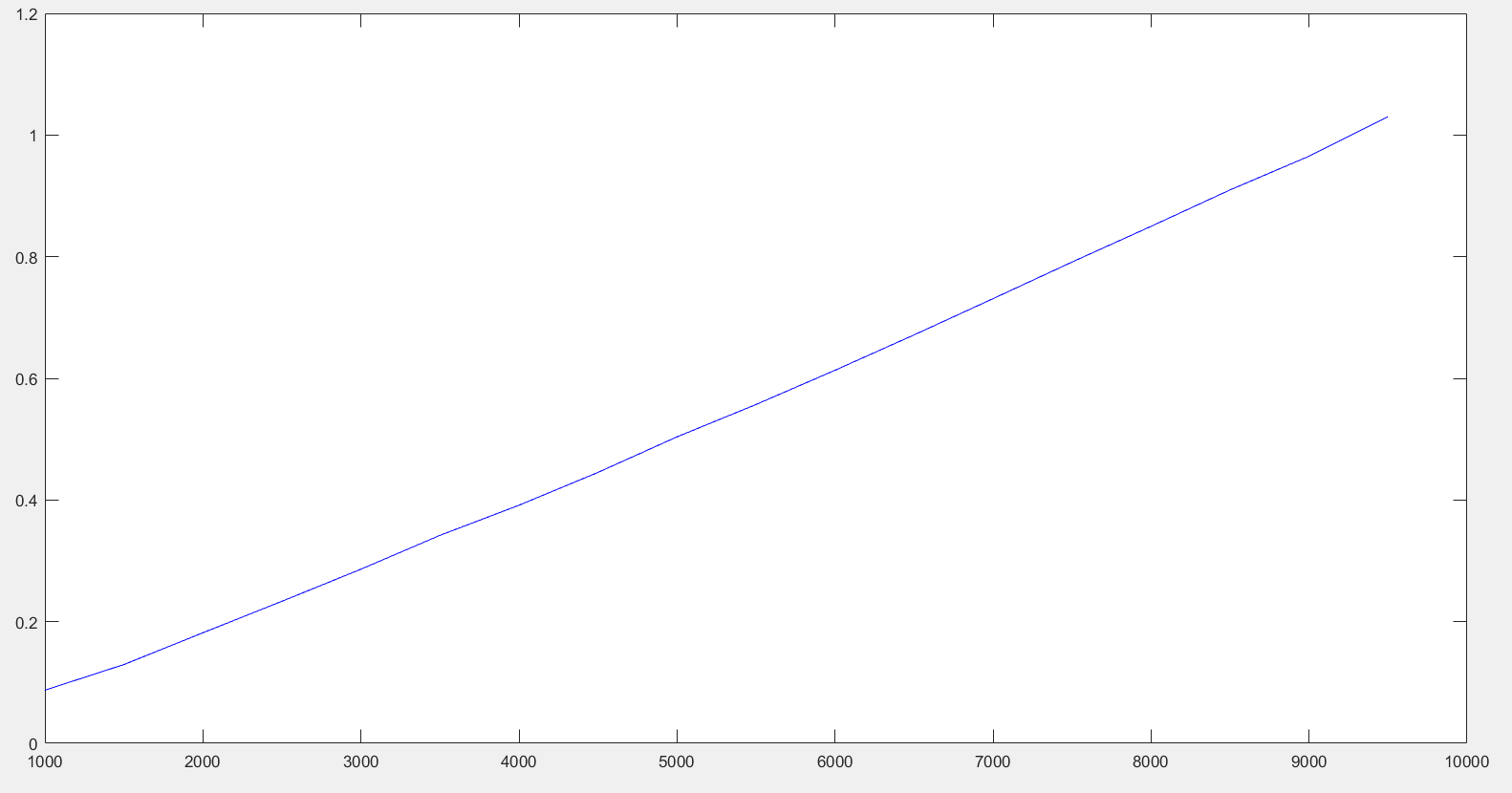
直接插入排序

  1. 时间复杂度分析

​ 堆排序也没有额外使用空间，无论是堆的初始化还是调整都是在数组中执行，移出堆只是一个逻辑上的，实际上还是在数组内，所以空间复杂度为O(1)。

冒泡排序

  1. 稳定性分析

​ 冒泡排序是稳定的，因为它永远是交换前后两个数，相同的数并不会交换。

  1. 时间复杂度分析

​ 冒泡排序的时间消耗主要在多次遍历未排序数组，每一次排序会排好一个数，所以一共需要进行n-1次排序,每一次遍历所经过的数据是从n-1递减1。但是可以对冒泡排序进行优化，如果某一次排序中不发生交换则意味着剩下的数据已经全部排序好。所以最好情况下为数据一开始就排序好，时间复杂度为O(n)，而最坏的就是最后一次才排序好，时间复杂度为O(n2)：

  • 最好情况:O(n)

  • 最坏情况:O(n^2^)

  • 平均情况:O(n^2^)

​ 在不同规模的情况下，使用运行程序测试方法来获取数据，将数据整合到下表

n的规模 运行时间(ms) n的规模 运行时间(ms)
1000 1.8016 5500 46.7417
1500 3.4543 6000 55.7510
2000 6.1377 6500 65.5473
2500 9.5916 7000 76.1662
3000 13.8146 7500 90.4104
3500 18.7863 8000 104.3133
4000 24.5685 8500 114.5724
4500 31.3092 9000 126.6079
5000 38.5921 9500 140.8599

根据数据绘制出对应的图像：

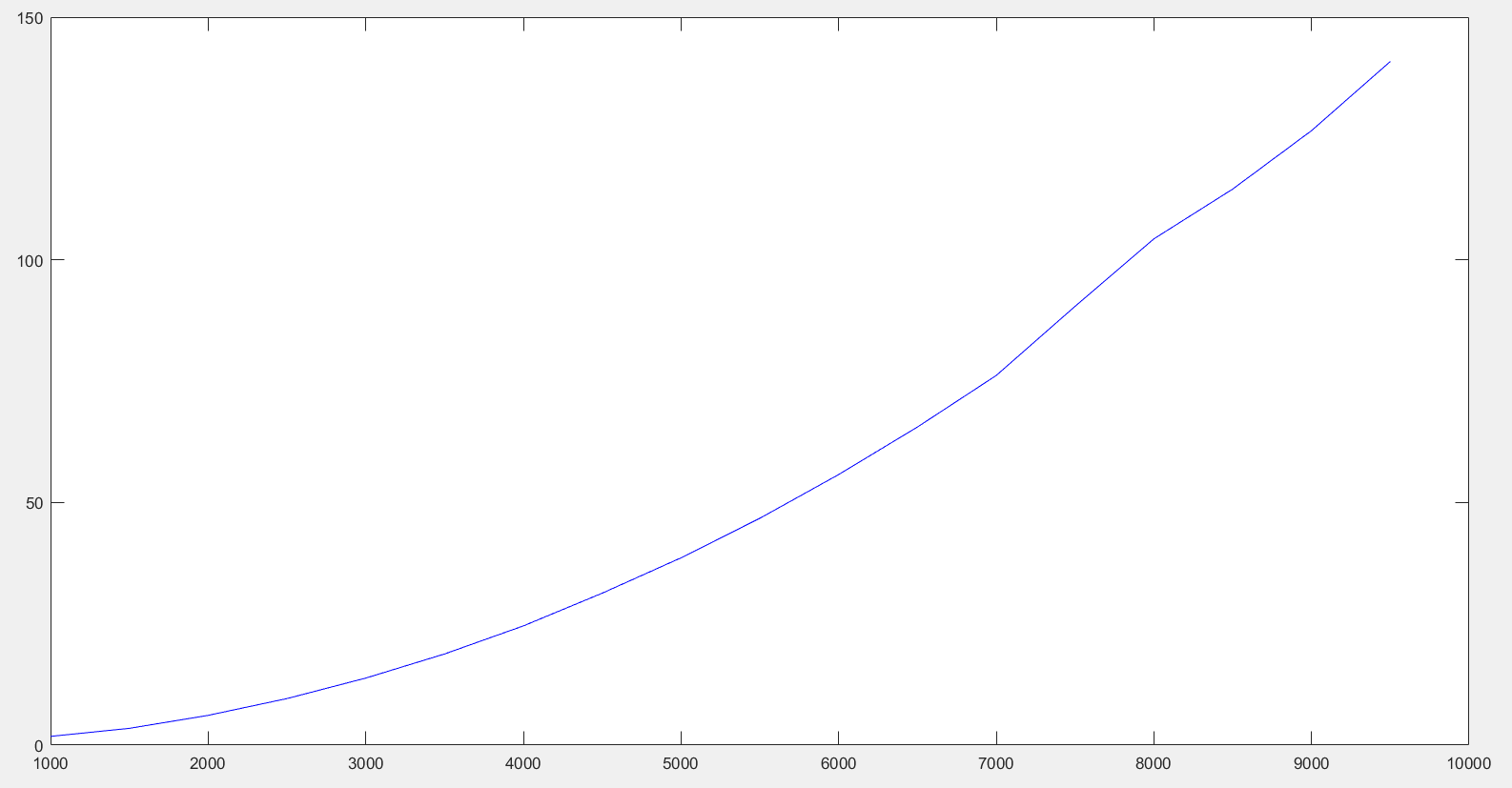
直接插入排序

  1. 时间复杂度分析

​ 冒泡排序也没有使用额外的空间，所以空间复杂度为O(1)。

快速排序

  1. 稳定性分析

​ 快速排序是不稳定的，因为在交换的过程中，可能把原来在前面的数交换到后面去。例如[5,9,4,7,9,2,6]，基准数是5，从右到左第一个比5小的是2，从左到右第一个比5大的是9，交换两者，就变成了[5,2,4,7,9,9,6],原来在前面的9被换到了后面去。

  1. 时间复杂度分析

​ 快速排序的时间消耗受子数据的分割影响。最好情况下，即每一次都对半分，则需要划分logn次，每一次遍历的长度从n对半递减到1，则时间复杂度为O(nlogn)。最坏情况下，每一次划分都是极端情况，即一份数据为0，一份数据为m-1(m为当前子数据的长度)，这种情况下，需要划分m-1次，每一次需要遍历的长度从m递降到2，则时间复杂度为O(n2)。通常情况下为时间复杂度为O(nlogn)。

  • 最好情况:O(nlogn)

  • 最坏情况:O(n^2^)

  • 平均情况:O(nlogn)

​ 在不同规模的情况下，使用运行程序测试方法来获取数据，将数据整合到下表

n的规模 运行时间(ms) n的规模 运行时间(ms)
1000 0.0687 5500 0.4293
1500 0.1034 6000 0.4724
2000 0.1393 6500 0.5178
2500 0.1802 7000 0.5594
3000 0.2183 7500 0.6043
3500 0.2576 8000 0.6529
4000 0.3025 8500 0.6915
4500 0.3443 9000 0.7400
5000 0.3859 9500 0.7832

根据数据绘制出对应的图像：

直接插入排序

  1. 时间复杂度分析

​ 快速排序虽然自身没有使用额外的空间来存储时间，但是递归时候将数据压入栈需要消耗空间，最好情况下为O(logn)，最坏情况下为O(n)，平均为O(logn)。

归并排序

  1. 稳定性分析

​ 归并排序是稳定的，虽然归并排序会把数据划分成左右两部分，但是在合并数据的时候，遇到相等的情况，可以先把左边的数据放在前面，这样就不会改变原来的先后次序。

  1. 时间复杂度分析

​ 归并排序的时间花费主要在于对子数据调用归并排序以及合并子数据。合并子数据只需要遍历一次数据，即O(n)。对子数据调用归并排序，每一次数据规模减半，直到数据为1，一共调用了logn次，每一次需要合并子数据的子数据，花费O(m)（m为子数据规模），综合起来，归并排序的时间复杂度为O(nlogn)。

  • 最好情况:O(nlogn)

  • 最坏情况:O(nlogn)

  • 平均情况:O(nlogn)

​ 在不同规模的情况下，使用运行程序测试方法来获取数据，将数据整合到下表

n的规模 运行时间(ms) n的规模 运行时间(ms)
1000 0.0908 5500 0.4907
1500 0.1191 6000 0.5404
2000 0.1593 6500 0.5897
2500 0.2029 7000 0.6409
3000 0.2499 7500 0.6921
3500 0.3007 8000 0.7346
4000 0.3465 8500 0.7928
4500 0.3999 9000 0.8431
5000 0.4382 9500 0.9049

根据数据绘制出对应的图像：

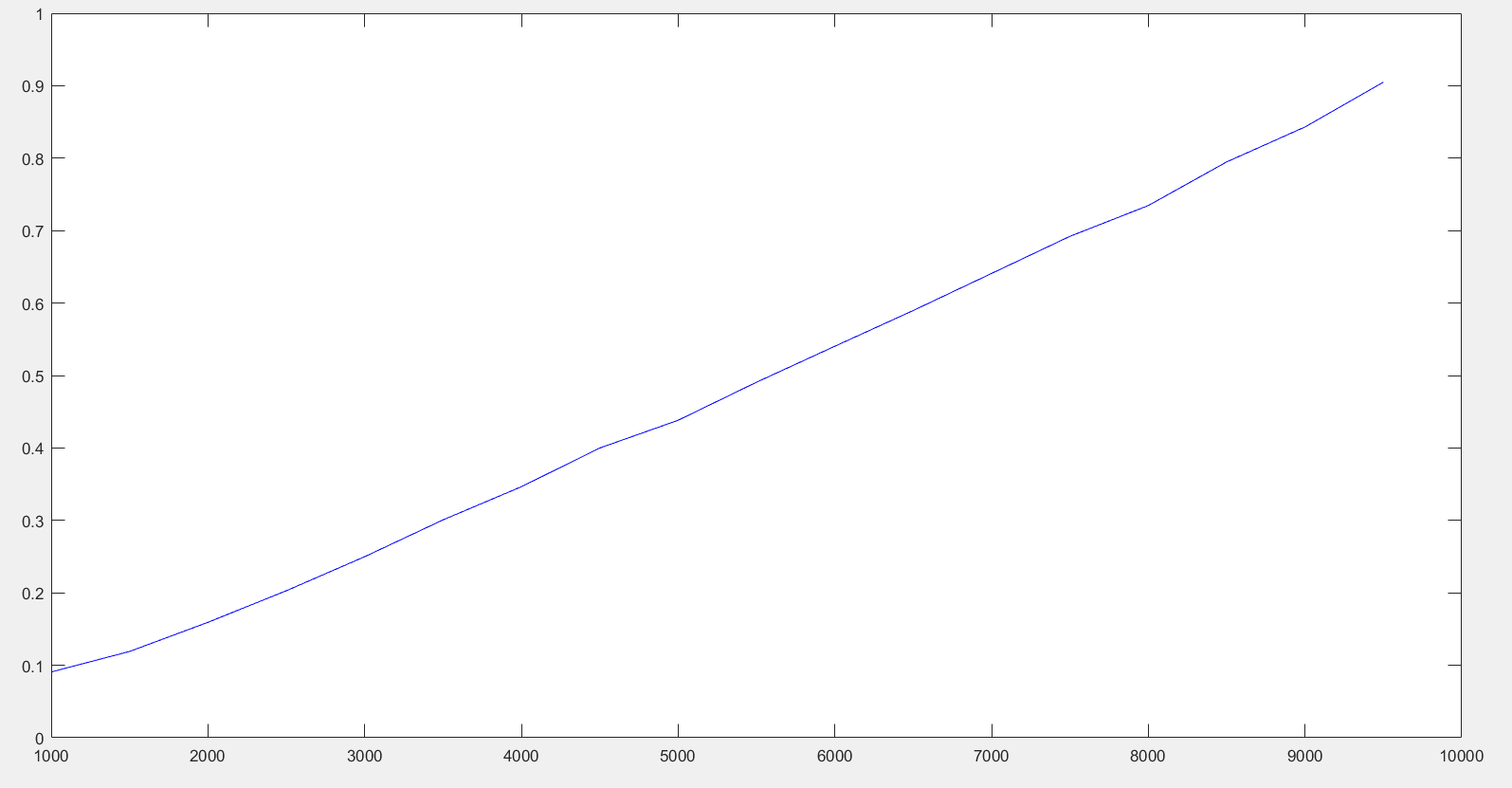
直接插入排序

  1. 时间复杂度分析

​ 归并排序的空间消耗主要是递归中将数据压入栈以及合并数据的时候使用的额外数组，一共会压入logn次栈，额外数组的长度最大为n，综合两者，归并排序的空间复杂度是O(n)。

基数排序

  1. 稳定性分析

​ 基数排序是稳定的，相同的数据会被分到同一个组，收集数据的时候也是从头开始收的，满足先进先出，所以基数排序是稳定的。

  1. 时间复杂度分析

​ 基数排序遍历数据k次，k为最大数据值的位数，每一次遍历所有数据，也就是n个，所以时间复杂度为O(k*n)。

  • 最好情况:O(k*n)

  • 最坏情况:O(k*n)

  • 平均情况:O(k*n)

​ 在不同规模的情况下，使用运行程序测试方法来获取数据，将数据整合到下表

n的规模 运行时间(ms) n的规模 运行时间(ms)
1000 0.0767 5500 0.3380
1500 0.0968 6000 0.3675
2000 0.1226 6500 0.3986
2500 0.1565 7000 0.4365
3000 0.1844 7500 0.4621
3500 0.2171 8000 0.4907
4000 0.2454 8500 0.5252
4500 0.2757 9000 0.5566
5000 0.3126 9500 0.5868

根据数据绘制出对应的图像：

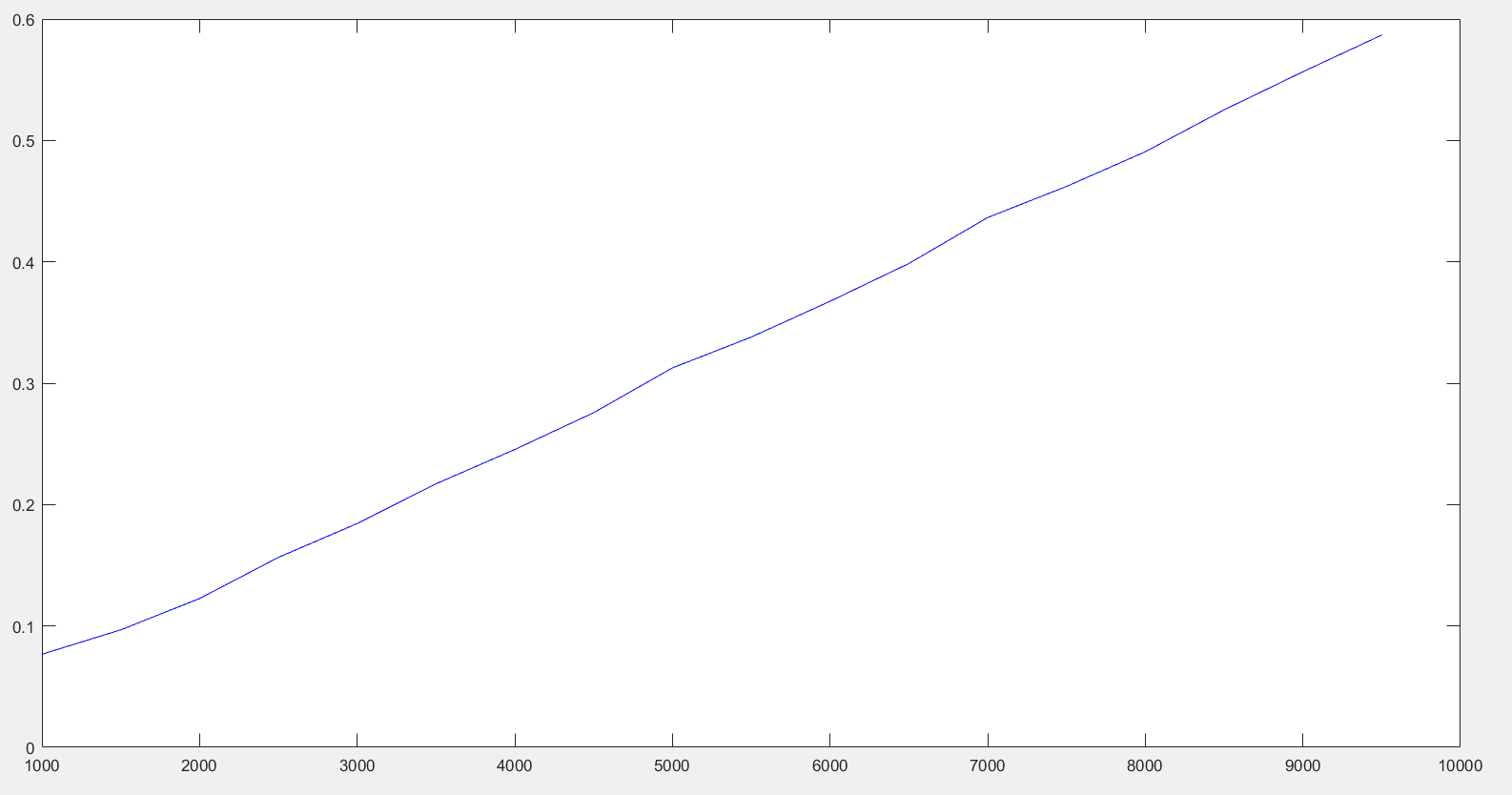
直接插入排序

  1. 时间复杂度分析

​ 基数排序需要先准备一个长度为10来计数以及一个大小为n的额外数组来存储数据，所以空间复杂度为O(n)。

排序算法的综合比较

​ 上述算法中除了希尔排序的数据略微不符合预期，其他的时间消耗曲线基本符合预期。希尔排序的时间消耗曲线虽然整体是上升的趋势，但是却不是那么平滑，甚至有些地方出现了比较突兀的转折。这是因为固定的增量和增长速度对不同的数据的影响不同，有些数据规模和它非常合适就运行的时间就比平均短。抛开个例，整体符合分析。

​ 将所有的数据整合到一张图，如下：

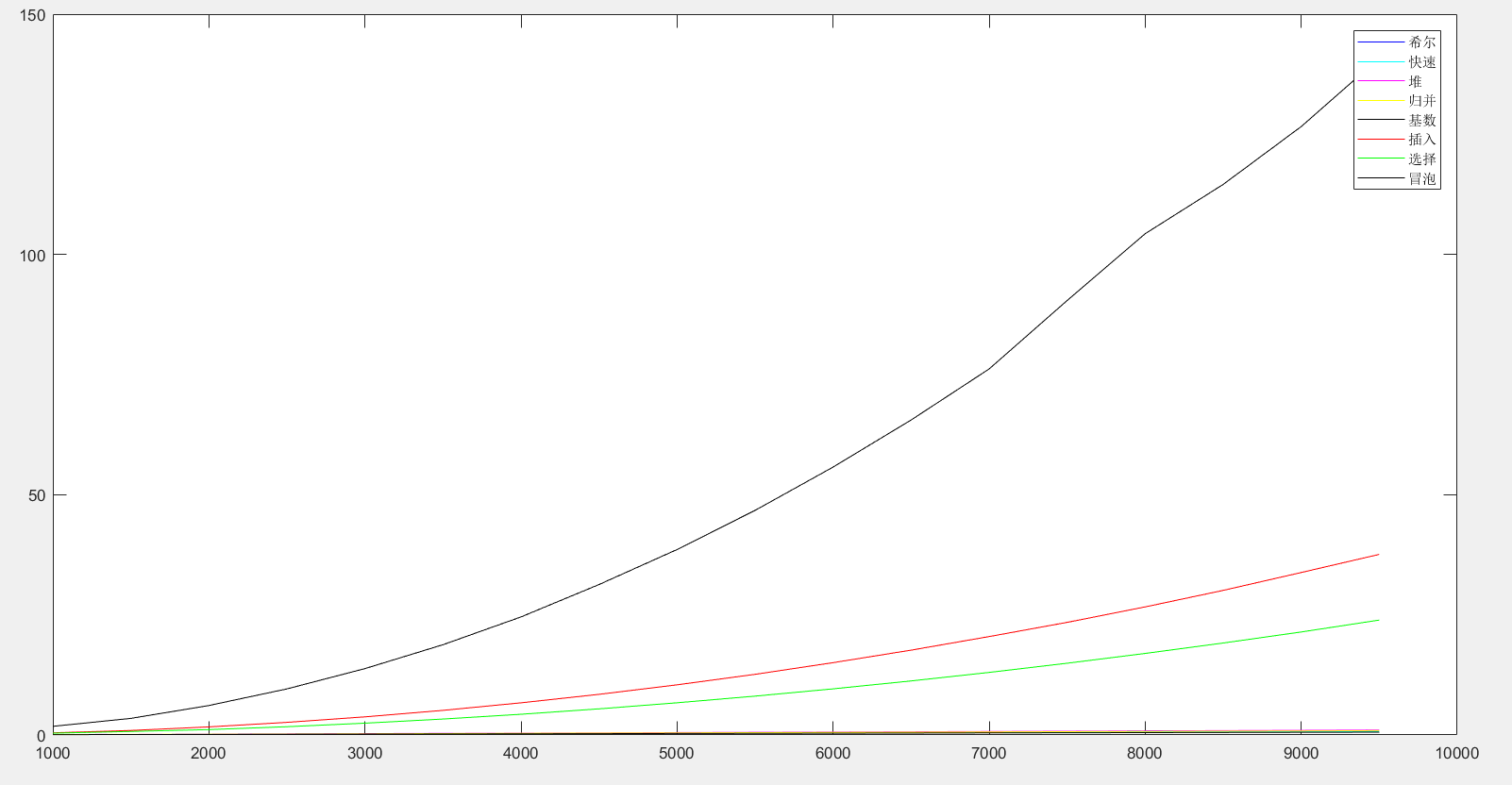
直接插入排序

​ 由于选择排序，插入排序和冒泡排序三者所消耗的时间远远超过其他排序，所以其他排序的时间消耗曲线看起来就像只有一条曲线。这三者中，选择排序的效率最好，接着是插入，最后是冒泡。三者的时间复杂度虽然都是O(n2)，但是不代表它们的效率是一样的，因为时间复杂度表示的是一个规模，他们都是O(n2)这个规模，但是系数以及其他的是不一样的。其中冒泡排序中有着大量的数据交换，时间消耗最高，插入则是部分交换，因此排第二，选择每一次只需要交换一次，所以时间消耗相对较低。

​ 去掉这三者以后再绘制一次图像，如下图：

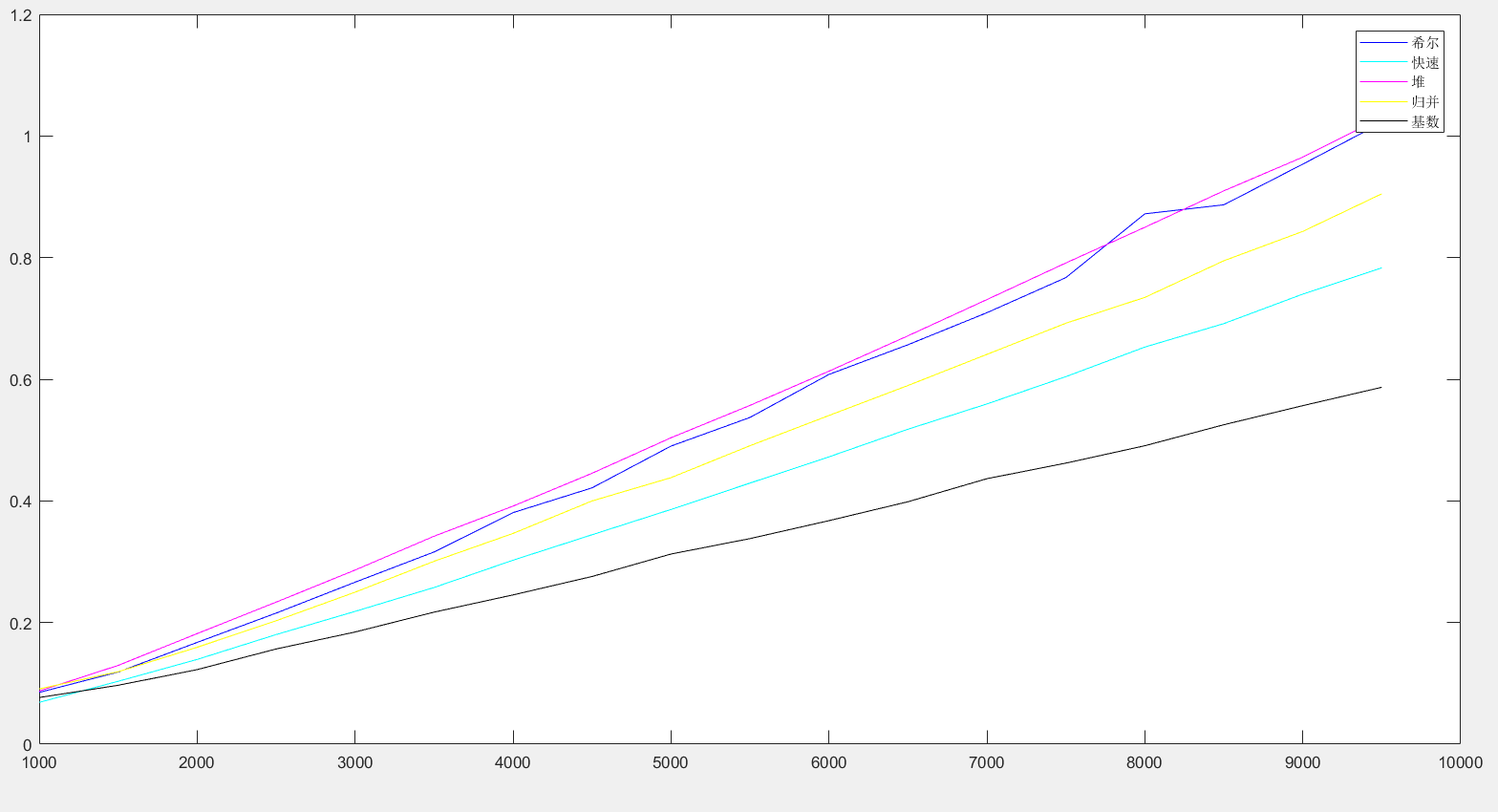
直接插入排序

​ 从图中可以看出基数排序的效率最好，快速次之，接下来是归并排序，然后希尔和堆排序的效率是差不多的。

为了进一步验证上面的结论，使用规模n为一千万的数据对这五者进行测试，运行的结果如下：

运行方法 时间消耗(ms)
基数排序 885
快速排序 1536
归并排序 1743
堆排序 3122
希尔排序 3572

​ 当数据规模大的时候，基数排序拥有远超其他排序的效率。快速排序和归并排序与上面分析一致，而堆排序则呈现出了比希尔排序（本文增量和增长速度的条件下）更好的效率。

将八个排序的基本信息汇集成一张表格，如下：

排序算法 时间复杂度平均情况 时间复杂度最好情况 时间复杂度最坏情况 空间复杂度 稳定性
插入排序 O(n2) O(n) O(n2) O(1) 稳定
希尔排序 O(nlogn) O(nlog2n) O(nlog2n) O(1) 不稳定
选择排序 O(n2) O(n2) O(n2) O(1) 不稳定
堆排序 O(nlogn) O(nlogn) O(nlogn) O(1) 不稳定
冒泡排序 O(n2) O(n) O(n2) O(1) 稳定
快速排序 O(nlogn) O(nlogn) O(n2) O(logn) 不稳定
归并排序 O(nlogn) O(nlogn) O(nlogn) O(n) 稳定
基数排序 O(k*n) O(k*n) O(k*n) O(n) 稳定

​ 在不考虑空间消耗的情况下，基数排序所消耗的时间低于其他排序，且数据规模越大，基数排序的优点就越明显，而且基数排序还是稳定的。

​ 既然这样，那么为什么普遍采用的是快速排序呢？

​ 借用算法导论中的说法，基数排序和快速排序时间复杂度但是隐含的常数项因子是不同的。在处理n个关键字时，尽管基数排序执行的循环轮数会比快速排序要少，但每一轮它所消耗的时间要长的多。哪一个排序算法更合适依赖于具体实现和底层硬件的特性（例如，快速排序通常可以比基数排序更有效的使用硬件的缓存），以及输入数据的特征，此外，利用计数排序作为中间稳定排序的基数排序不是原址排序，而很多O(nlogn)时间的比较排序是原址排序。因此，当主存内存比较宝贵时，我们可能更倾向于像快速排序这样的原址排序算法。

一些其他的话

​ 快速排序是应用及其广泛的算法，除去不稳定之外，它基本是最优秀的排序算法，极好的运行效率，较少的内存占用，原址排序等，在编程中，如果我们不知道什么算法比较适合自己的程序，不妨先尝试一下快速排序。

本文存在诸多问题，例如时间复杂度的分析略显简单，没有很系统的说明，各算法所消耗的空间资源无法简单的计算，需要比较专业的软件。数据的统计已经尽力控制在相同环境以及尽可能运行多次来减少误差，但是还是有小部分数据出现不符合预期的情况。各算法是我自己实现，不能保证该算法是否达到自身效率的极限，例如快速排序没有进行优化。

​ 所以本文只是浅析，如有错误，可以私信我(通过QQ)

赏

谢谢你的心意

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

Jeislu<br><br>一只广财在读，努力摆脱懒惰的菜鸡<br>希望我每天都可以多学一点